Y-Wing can be a very handy shortcut in a tough sudoku puzzle and it may even be the only way forward in some harder ones. It’s named after an ugly rebel fighter craft from the Star Wars movies. True to its namesake, it is not as elegant or as powerful as its X-Wing brother, but it can still do some damage.
Y-Wing can be hard to spot, so today I’ll describe a method for quickly teasing out the best ones. It boils down to this — the best Y-Wing sets are the ones where two of the three squares in the set are in the same 3×3 box!
Really, don’t bother looking for a set that’s super spread-out. It’s very rare that you’ll find one and even if you do, it’s the weakest kind: you’ll only be able to remove one candidate from one square, and that’s if you’re lucky.
Y-What?
First, let’s make sure we all know what we’re looking for. The basic idea is, you find three squares that each have two remaining candidates. The “pivot” square can see both of the end squares. All three squares share candidates from a pool of just three total numbers, ABC. So one end of the “V” is AB, the pivot has BC, and the other end is AC.
Important detail – no two squares in the set have the same pair of candidates. So, if you whittle down three squares to 78, 48 and 47, you’re well on your way to a Y-Wing. If you’re looking at 47, 48 and 47, no deal.
Any square that can see both ends of the Y-Wing may eliminate candidate A from its own candidate pool. It’s an easy proof, just look at the pivot — when the puzzle is done, the pivot will either be B or C.
If the pivot is B, then the first end is not B, and must be A. In the other “reality,” if pivot is C, then the other end is not C, and must be A. Since the pivot must be either B or C, at least one of those end squares will have A. Here’s the neat part: squares that can “see” both end squares can never be A; not in the first case, and not in the second case (and there are only two cases total).
The Claw
Some people like to think of Y-Wing as a claw. A simple way to visualize it is, the claw’s pincers (end squares) “pinch” candidate A out of any square they can both see. The pivot is the “hinge” of the claw.
There are two kinds of Y-Wing. One can be very helpful, and one is usually not. If the three squares in your Y-Wing are all in different boxes, you’ve found the less useful Y-Wing variant (your claw is wide open, pincers at 90 degrees). Only one square can see both pincers – so even if we are lucky, we can only eliminate/pinch one candidate from one square.
The kind I like is when one claw pincer and the pivot share a box. Then you’ll always have more than one “pinchable” square (up to five, in fact). Fortunately, finding this second type is easier anyway.
The Method
Look at each group of 9 squares (the nine large 3×3 boxes). In each big box, look for two squares in that box with only two candidates left each. They must share exactly one candidate. It’s okay if they are in the same row/column but you’ll cast a wider net for the other claw if they aren’t. Found a pair like this? Good. Now look at the two candidates they don’t have in common. Let’s call them AB. We are looking for a third square, from a different box, that has only AB left in its candidate pool. It must be able to “see” one of our original squares (yep, either one). The square that it sees from our original box becomes the pivot.
So, we really just scan four potential zones outside our box:
• the squares in the same row as square 1
• the squares in the same row as square 2
• the squares in the same column as square 1, and finally,
• the squares in the same column as square 2
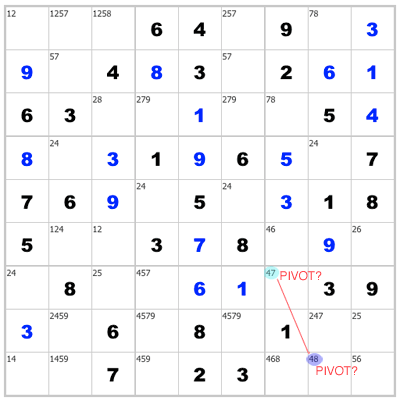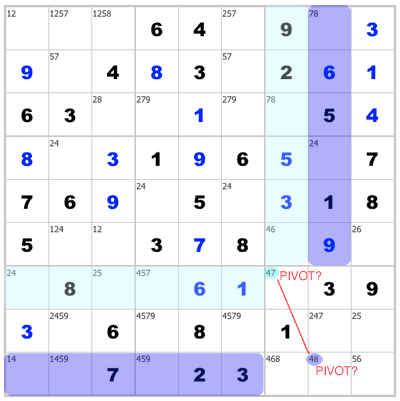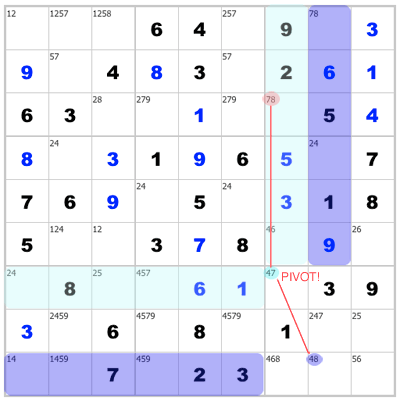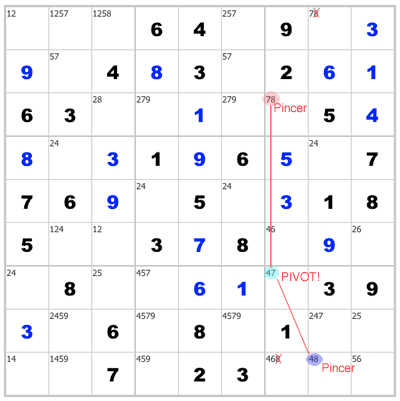
Didn’t pan out? Move along, find another potential pivot/claw pair, maybe in this box or probably the next. You’d be surprised how often you can track down a set of three once you focus your search like this. See if you can find the Y-Wing below. hint: start in box 7.
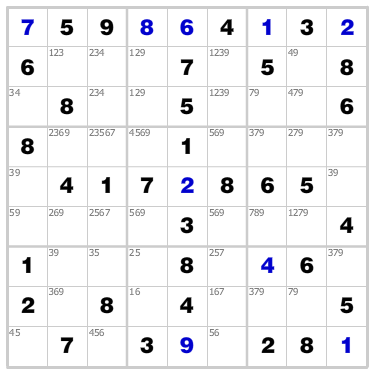
Y-Wing Example